Numpy矩阵运算
0. 概要
本文讲解了numpy的一些基础操作,同时还介绍了numpy中两个重要的概念,全局函数与广播。最后还介绍了numpy下面的两个包,linalg线性代数计算包与random随机生成包。
1. Numpy简介

NumPy是一个运行速度非常快的数学库,主要用于矩阵运算。NumPy是Python在科学计算领域取得成功的关键之一,如果你想通过Python学习数据科学,就必须学习NumPy。
为什么我们不用python原生的list呢?
-
矩阵运算功能
NumPy可以让你在Python中使用向量和数学矩阵,它封装了很多矩阵运算操作,这些都是list所不具备的。
-
numpy更省空间
NumPy中数组的存储效率和输入输出性能均远远优于Python中等价的基本数据结构,且能够提升的性能是与数组中的元素成比例的。
-
处理速度更快
NumPy的大部分代码都是用C语言写的,其底层算法在设计时就有着优异的性能,这使得NumPy比纯Python代码高效得多。
关于这方面的讨论细节,大家可以在StackOverflow上的一篇问答中了解更多:
2. 安装Numpy
在Windows下安装Numpy
pip install numpy
在Linux下安装Numpy
sudo pip3 install numpy
3. 引入Numpy模块
引入numpy模块
🖌 代码片段
import numpy
习惯上,我们引入numpy模块时,会将numpy起一个别名
np
,方便调用 (因为比较简短)
🖌 代码片段
import numpy as np
4. 设置打印选项
设置打印选项,让打印出来的数组可读性更强。
🖌 代码片段
# 设置Numpy的打印选项
# precision: 浮点数精确位数
# suppress:
# - True: 固定浮点 、
# - False: 使用科学计数法
np.set_printoptions(precision=3, suppress=True)
在配置完成后,生成一个长度为10的随机数组
print(np.random.rand(10))
📓 输出日志
[0.469 0.484 0.284 0.089 0.156 0.431 0.479 0.737 0.825 0.921]
5. 数组初始化
NumPy的核心是多维数组 (ndarrays: n-dimension array)。
使用
np.array
函数初始化几个数组,声明数组的方法就是使用
[]
嵌套,
,
分割同层级的元素。
创建一个一维数组
🖌 代码片段
# 一维数组
A1 = np.array([1, 2, 3])
print("A1 :\n{}".format(A1))
📓 输出日志
A1 : [1 2 3]
创建一个二维数组
🖌 代码片段
# 二维数组
A2 = np.array([[1, 2, 3], [4, 5, 6]])
print("A2 :\n{}".format(A2))
📓 输出日志
A2 : [[1 2 3] [4 5 6]]
6. 数组的属性
这里给大家展示几个常用的属性:
| 属性名称 | 含义 |
|---|---|
| ndarray.ndim | 数组的维度,等于Rank |
| ndarray.shape | (行数, 列数) |
| ndarray.size | 元素总个数 = 列数 * 行数 |
| ndarray.dtype | 数组元素数据类型 |
| ndarray.itemsize | 数组中每个元素,字节大小 |
🖌 代码片段
print('A2.ndim = %d' % A2.ndim)
print('A2.shape')
print(A2.shape)
print('A2.size = %d' % A2.size)
print('A2.dtype = %s' % A2.dtype)
print('A2.itemsize = %d' % A2.itemsize)
📓 输出日志
A2.ndim = 2 A2.shape (2, 3) A2.size = 6 A2.dtype = int32 A2.itemsize = 4
7. 数组的数据类型
dtype
numpy
的ndarray所有的元素数据类型必须相同,这是为矩阵运算做保障的。
Python支持的数据类型有整型、浮点型、复数型,但这些类型不足以满足科学计算的需求,因此NumPy中添加了许多其他的数据类型,如:bool、inti、int64、float32、complex64等。同时,它也有许多其特有的属性和方法。
在Numpy中定义了24种新的Python基础数据类型,大多基于 C语言 的数据类型。
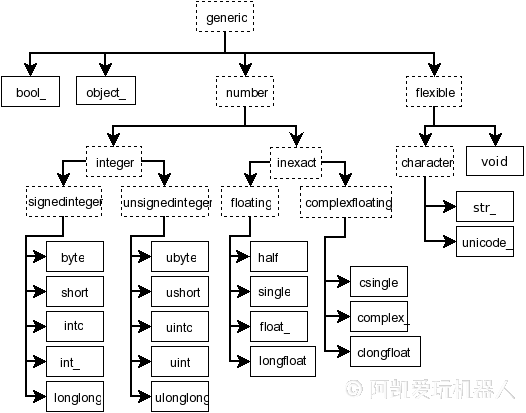
我们还可以使用
astype
函数,将原本为int类型的
ndarray
转换为浮点型。
🖌 代码片段
A = np.array([[1, 2, 3], [4, 5, 6]])
print("转换前的格式: A.dtype = {}".format(A.dtype))
print("A:\n {}".format(A))
# 修改数据格式
A = A.astype("float32")
print('转换后 A.dtype = {}'.format(A.dtype))
print("A:\n {}".format(A))
📓 输出日志
转换前的格式: A.dtype = int32 A: [[1 2 3] [4 5 6]] 转换后 A.dtype = float32 A: [[1. 2. 3.] [4. 5. 6.]]
8. 等差数列
8.1 整数等差数列
初始化一个数组,我们还可以使用"批量"的方式,
np.arange
的使用方法类似Python原生的
range
。
函数原型
arange([start,] stop[, step,], dtype=None)
-
start:数值区间开始,默认是0 -
stop:数值区间结束 -
step:数值增加间隔,默认为1 -
dtype:数据类型
🖌 代码片段
print('递增数列: ')
print(np.arange(0, 10, 1))
📓 输出日志
递增数列: [0 1 2 3 4 5 6 7 8 9]
如果不传入
start
则模式从
0
开始
🖌 代码片段
print(np.arange(10))
📓 输出日志
[0 1 2 3 4 5 6 7 8 9]
我们接下来实验一下 递减
🖌 代码片段
print('递减数列')
print(np.arange(10, 0, -1))
📓 输出日志
递减数列 [10 9 8 7 6 5 4 3 2 1]
8.2 浮点数等差数列
我们还可以使用
linspace
在一个数值区间内划分若干个段 (浮点数)。
注意第三个参数为插值点的个数。
🖌 代码片段
# 随机间隔
np.linspace(0, 10, 5)
📓 输出日志
array([ 0. , 2.5, 5. , 7.5, 10. ])
9. 数组变形

在矩阵计算中,有时我们需要将矩阵进行变形,例如原来是
4*5
的矩阵,可能会变形为
5*4
或者
10*2
。
也有可能改变维度,原来是二维的转变为一维的,例如
1*20
。
这里我们就需要两个函数
resize
和
reshape
定义一维数组
🖌 代码片段
A = np.arange(10)
📓 输出日志
[0 1 2 3 4 5 6 7 8 9]
9.1 reshape
reshape
函数变形前与变形后的
size
必须相同,否则就会报错。
ndarray
对象
A
在调用
reshape
函数时, 返回一个新的ndarray对象,原来的ndarray并不发生改变。
reshape函数的原型:
reshape(a, newshape, order='C')
-
a:是要被resize的数组 -
new_shape:是新数组的尺寸,类型为tuple元组类型
使用样例
🖌 代码片段
new_dim = (2,5) # 新的数组维度
B = np.reshape(A, new_dim)
print("B 尺寸: {}".format(B.shape))
print(B)
print("A 尺寸: {}".format(A.shape))
print(A)
📓 输出日志
B 尺寸: (2, 5) [[0 1 2 3 4] [5 6 7 8 9]] A 尺寸: (10,) [0 1 2 3 4 5 6 7 8 9]
另外还可以在数组后调用reshape函数,效果与使用
np.reshape
是一样的。
🖌 代码片段
B = A.reshape(new_dim)
9.2 resize
np.resize的函数原型
resize(a, new_shape)
-
a:要被resize的数组 -
new_shape:新数组的尺寸,类型为tuple元组类型
使用
np.resize
的效果,与
np.reshape
的效果是类似的。
🖌 代码片段
B = np.resize(A, new_dim)
print("B 尺寸: {}".format(B.shape))
print(B)
print("A 尺寸: {}".format(A.shape))
print(A)
📓 输出日志
B 尺寸: (2, 5) [[0 1 2 3 4] [5 6 7 8 9]] A 尺寸: (10,) [0 1 2 3 4 5 6 7 8 9]
A.resize(new_dim)
函数会直接在原来的数组里面修改,不会返回新的数组。
🖌 代码片段
A.resize(new_dim)
print("A 尺寸: {}".format(A.shape))
print(A)
📓 输出日志
A 尺寸: (2, 5) [[0 1 2 3 4] [5 6 7 8 9]]
10. 线性代数运算
np.linalg
numpy的
linalg
里包含着线性代数的函数。
引入linalg模块
,引入并起名为
LA
🖌 代码片段
import numpy.linalg as LA
声明一个矩阵
A
🖌 代码片段
A = np.random.rand(16).reshape((4, 4))
📓 输出日志
[[0.477 0.084 0.615 0.226] [0.009 0.246 0.653 0.785] [0.752 0.377 0.395 0.335] [0.03 0.997 0.114 0.243]]
10.1 矩阵转置
🖌 代码片段
print(A.T)
📓 输出日志
[[0.477 0.009 0.752 0.03 ] [0.084 0.246 0.377 0.997] [0.615 0.653 0.395 0.114] [0.226 0.785 0.335 0.243]]
10.2 矩阵求逆
🖌 代码片段
LA.inv(A)
📓 输出日志
[[-0.572 -0.414 1.717 -0.499] [ 0.3 -0.344 -0.232 1.15 ] [ 2.974 -0.207 -1.903 0.521] [-2.563 1.559 1.637 -0.788]]
10.3 矩阵乘法
另外声明一个矩阵 B
🖌 代码片段
# 创建矩阵B
B = np.random.rand(8).reshape((2, 4))
print("B = \n{}".format(B))
📓 输出日志
B = [[0.401 0.394 0.528 0.917] [0.513 0.735 0.289 0.533]]
矩阵相乘
dot
🖌 代码片段
print(B.dot(A))
📓 输出日志
[[0.619 1.244 0.817 0.799] [0.485 0.864 0.97 0.919]]
10.4 行列式求解
🖌 代码片段
print(LA.det(A))
📓 输出日志
0.1799090776573458
11. 随机数
np.random
11.1 生成整数随机数组
🖌 代码片段
# 随机生成2x3的矩阵,矩阵元素取值范围 [low, high)
np.random.randint(low=0, high=100, size=(2,3))
📓 输出日志
array([[24, 13, 88], [14, 22, 61]])
11.2 生成0-1区间的浮点数随机数组
🖌 代码片段
print('生成10个0-1区间内的随机数值')
print(np.random.rand(10))
📓 输出日志
生成10个0-1区间内的随机数值
[0.638 0.477 0.969 0.186 0.692 0.245 0.162 0.877 0.457 0.051]
11.3 生成满足正态分布的随机数组
🖌 代码片段
print('生成10个满足正态分布的随机数组')
print(np.random.randn(10))
📓 输出日志
生成10个满足正态分布的随机数组 [ 0.26 -0.702 0.107 -0.105 -2.571 -0.665 0.632 -2.242 -1.283 0.924]
11.4 打乱排序
🖌 代码片段
A = np.arange(10)
print("A = {}".format(A))
np.random.shuffle(A)
print("打乱顺序后\n A = {}".format(A))
📓 输出日志
A = [0 1 2 3 4 5 6 7 8 9] 打乱顺序后 A = [0 5 3 4 9 2 7 6 8 1]
11.5 随机抽样
从数组A中随机抽取两个元素
🖌 代码片段
np.random.choice(A, size=2)
📓输出日志
array([7, 3])
12. 全局函数
ufunc
作用于数组中每个元素的函数我们称之为
ufunc
,英文全称为universal function。只有维度相等的两个数组才能进行全局函数运算。
常用的全局函数如下:
-
+加法 -
-减法 -
*乘法,注意这里不是点乘 -
/除法 - 三角函数,数学函数
声明两个尺寸相同的矩阵。
A
与
B
🖌 代码片段
# 随机生成2x3的矩阵,矩阵元素取值范围 [low, high)
A = np.random.randint(low=0, high=10, size=(3,3))
B = np.random.randint(low=0, high=10, size=(3,3))
print("A \n{} \nB\n{}".format(A, B))
📓 输出日志
A [[7 9 5] [5 3 0] [1 5 9]] B [[5 1 8] [4 6 6] [1 4 6]]
12.1 全局加法
🖌 代码片段
A + B
📓 输出日志
array([[12, 10, 13], [ 9, 9, 6], [ 2, 9, 15]])
12.2 全局减法
🖌 代码片段
A - B
📓 输出日志
array([[ 2, 8, -3], [ 1, -3, -6], [ 0, 1, 3]])
12.3 全局乘法
🖌 代码片段
A * B
📓 输出日志
array([[35, 9, 40], [20, 18, 0], [ 1, 20, 54]])
12.4 全局除法
🖌 代码片段
A / B
📓 输出日志
array([[1.4 , 9. , 0.625], [1.25 , 0.5 , 0. ], [1. , 1.25 , 1.5 ]])
12.5 其他全局函数
如果我们的计算对象是单个ndarray中的每个元素,就需要使用到numpy内置的一些全局函数。
例如
np.sin()
,这个函数的作用就是返回一个矩阵,其中每个元素都是原来矩阵
A
进行
sin
运算的结果。
🖌 代码片段
np.sin(A)
📓 输出日志
array([[ 0.6569866 , 0.41211849, -0.95892427], [-0.95892427, 0.14112001, 0. ], [ 0.84147098, -0.95892427, 0.41211849]])
13. 索引操作
Index
何为索引?

一开始这里是一个大大的面包,而我们需要这一整个面包其中的一部分,所以为了达到这个目的,我们要进行索引,可以横着切,也可以竖着切,于是我们就获得了面包片。同样对于多维数组,我们索引是为了获取数组中的一个子区域。
13.1 一维数组索引
Numpy中多维数组的索引操作与Python中list的索引操作一样,同样由
start
,
stop
,
step
三个部分组成。
首先我们声明一个长度为10的一维数组。
🖌 代码片段
A = np.arange(10)
我们需要获取前三个元素
输入
A[:3]
,使用
:
分隔,第一个参数是起始值,默认为0,这里可以省略。后面的
3
是索引的结尾 (但是取不到编号为3的元素)。
🖌 代码片段
A[:3]
📓 输出日志
array([0, 1, 2])
完整版是这种写法:
🖌 代码片段
A[0:3]
📓 输出日志
array([0, 1, 2])
13.2 多维数组索引
针对多维数组的索引,不同之处在于,需要使用
,
分隔。
一图胜千言,相信大家看下面这张图片就会秒懂。
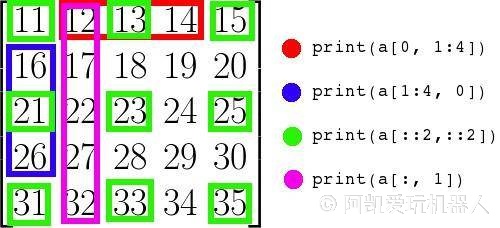
14. 矩阵拼接
在opencv中常会用到图像拼接,这里就需要用到numpy中的矩阵拼接。
矩阵拼接有个前提条件,就是拼接的那一面长度必须相同。
-
hstack()横向拼接 -
vstack()纵向拼接
我们先声明两个矩阵,
A
,
B
🖌 代码片段
A = np.arange(16).reshape(4,4)
B = np.arange(16).reshape(4,4) * -1
print("A: \n{}".format(A))
print("B: \n{}".format(B))
📓 输出日志
A: [[ 0 1 2 3] [ 4 5 6 7] [ 8 9 10 11] [12 13 14 15]] B: [[ 0 -1 -2 -3] [ -4 -5 -6 -7] [ -8 -9 -10 -11] [-12 -13 -14 -15]]
然后将两个矩阵先进行 横向拼接 , 注意这里传入的是tuple 。
🖌 代码片段
# 注意这里传入的是tuple
np.hstack((A, B))
📓 输出日志
array([[ 0, 1, 2, 3, 0, -1, -2, -3], [ 4, 5, 6, 7, -4, -5, -6, -7], [ 8, 9, 10, 11, -8, -9, -10, -11], [ 12, 13, 14, 15, -12, -13, -14, -15]])
然后再尝试进行 纵向拼接 。
🖌 代码片段
np.vstack((A, B))
📓 输出日志
array([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11], [ 12, 13, 14, 15], [ 0, -1, -2, -3], [ -4, -5, -6, -7], [ -8, -9, -10, -11], [-12, -13, -14, -15]])
15. 内存共享与深度拷贝
如果将一个ndarray直接赋值给另外一个ndarray,那么这两个元素所使用的内存都是同一块。也就意味着,如果A = B,修改B的值,A也会被修改,因为他们共用了同一片内存空间。这样比较高效,但是如果不注意的话,也会造成很多问题。
创建一个数组A,将B赋值为A,并修改B中元素的取值
🖌 代码片段
A = np.array([[1, 2], [3, 4]])
B = A
B[0][0] = -1
print("A =\n {}".format(A))
print("B =\n {}".format(B))
📓 输出日志
A = [[-1 2] [ 3 4]] B = [[-1 2] [ 3 4]]
可以看到A和B的值都被修改了。
那么,我们如何才可以复制一个ndarray,修改新的ndarray而不影响之前的值呢?
这里我们需要用到numpy的深度拷贝函数
np.copy
🖌 代码片段
A = np.array([[1, 2], [3, 4]])
B = np.copy(A)
B[0][0] = -1
print("A =\n {}".format(A))
print("B =\n {}".format(B))
📓 输出日志
A = [[1 2] [3 4]] B = [[-1 2] [ 3 4]]
当然我们也可以使用另外一种拷贝方式:
🖌 代码片段
B = A.copy()
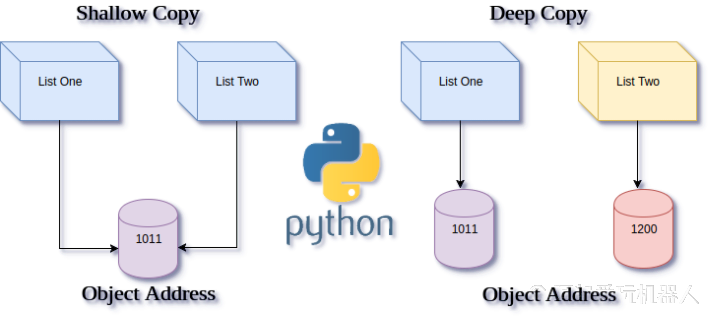
如果你对python中的浅度拷贝和深度拷贝不是很清楚的话,可以看一下博客园的这篇文章:
图解Python深拷贝和浅拷贝
。了解一下copy包里面的
copy
和
deepcopy
两个函数有哪些不同。